Badania epidemiologiczne są kosztowne, żmudne i długotrwałe, a koniec końców nic nie mówią o jednostce, tylko o populacji. Pomiary fizyczne są dokładne, ale prostopadłościan z wody to słabe przybliżenie człowieka, a pomiar we wnętrzu żyjącego organizmu punkt przy punkcie jest praktycznie niewykonalny (jeśli ten ma pozostać przy życiu…). To skąd wiedzieć co się dzieje np. w mózgu, gdy rozmawiamy przez telefon? Tu z pomocą przychodzą symulacje komputerowe! Tylko jak „włożyć” do nich człowieka? I co to jest perfuzja?!
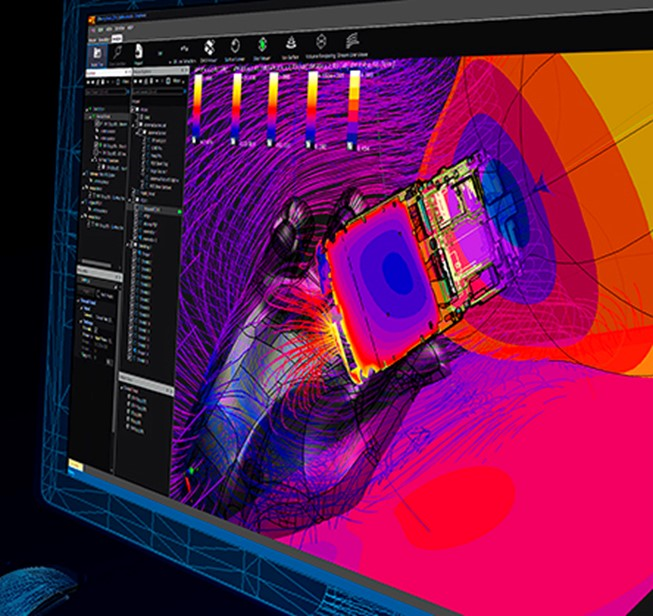
Aby obliczyć ilościowo wpływ promieniowania elektromagnetycznego na żywy organizm, potrzebujemy ustalić trzy podstawowe kwestie. Po pierwsze – jakie dokładnie promieniowanie symulujemy, ponieważ z częstotliwością zmieniają się mechanizmy oddziaływań fizycznych. Po drugie – co będzie symulowanym obiektem, czyli jak złożony będzie nasz fantom. Po trzecie – co właściwie chcemy wyznaczyć? Okazuje się, że w danej tkance takie wielkości jak „ilość pochłoniętej energii” i „wzrost temperatury” wcale nie muszą się pokrywać…
Kto by tam liczył analitycznie…
Przy częstotliwościach telekomunikacyjnych będą nas najbardziej interesować efekty termiczne. Ale zanim do nich dojdziemy, to najbardziej fundamentalną sprawą jest rozwiązanie układu równań Maxwella – wszak to one opisują zachowanie się pól elektromagnetycznych. Tyle, że… no wiecie, gradienty, rotacje, pochodne cząstkowe… nikt nie siada do tego z kartką i długopisem! Zaprzęga się do tego komputery, tyle że im trzeba zapodać odpowiednie algorytmy. Rzeczywiste zagadnienia najczęściej są zbyt złożone, aby podać rozwiązanie analityczne (np. że czas spadania kulki z wysokości H przy pominięciu oporu powietrza to 
), dlatego stosuje się metody numeryczne. Tu wchodzi FDTD, cała na biało, czyli Metoda Różnic Skończonych w Dziedzinie Czasu opisana przez Kane’a Yee w 1966r. Szczegółowy algorytm znajdziecie w [1], ale w skrócie chodzi o podział badanej przestrzeni na malutkie kawałki i obliczaniu lokalnych wartości natężeń pól w każdym z nich. Wartości muszą spełniać warunki brzegowe, tzn. wektory na dwóch przylegających do siebie ściankach muszą być takie same – ale teraz sprawa jest prostsza, bo wystarczy proste obliczenie powtórzyć N razy.
Ale jak wygląda człowiek?
Wiemy, jak liczyć propagację fal EM w małych elementach przestrzeni – ale trzeba tę przestrzeń czymś zapełnić. Pytanie zatem co będzie naszym fantomem, czyli obiektem, na który te fale będą oddziaływać. Wersja najprostsza – sześcian z wodą – jest dobra do ćwiczeń i porównania otrzymanych wyników z eksperymentem (wkładamy czuły termometr do wody, w którą „strzelamy” określoną wiązką z anteny), ale pomija złożoność docelowego układu, czyli człowieka. Tu pojawia się szereg problemów i pomysłów – ot choćby jak duży powinien być voxel:
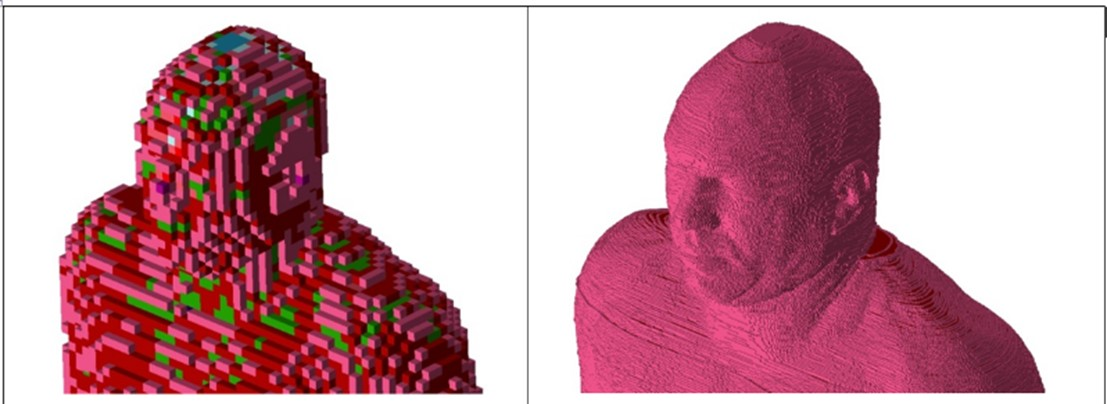
Jasne, że im mniejszy voxel, tym lepsza rozdzielczość, ale im mniejszy voxel, tym więcej voxeli – zatem trzeba dłużej liczyć. Coś za coś, ale czas potrzebny do obliczeń to nie wszystko, istotne jest jeszcze jak się ma rozmiar voxela do rozmiaru padającej fali! Ale i tak schody są dopiero przed nami: jakie parametry ma mieć dany voxel, czyli jakie własności ma tkanka, której on odpowiada? Tu sięgamy do tablic i każdej „tkance” w modelu numerycznym przypisujemy odpowiednią przenikalność elektryczną, znaną eksperymentalnie z pomiarów. A skąd wiedzieć gdzie jest jaka tkanka? Tu możemy sięgnąć do skanów tomografii komputerowej – efekty są spektakularne:
Jeśli ten poziom szczegółowości nadal Was nie rzucił na kolana i będziecie argumentować, że przecież ludzie są różni, to ripostuję – tak, są różni, dlatego możecie przywitać się z całą rodziną fantomów przygotowanych przez szwajcarskich naukowców. Płeć, wiek, wzrost, otyłość, wszystko uwzględnione:
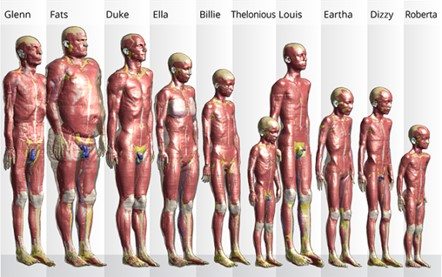
Skoro wiemy, jaka fala elektromagnetyczna pada na jakie tkanki (o jakich własnościach dielektrycznych), to możemy obliczyć podstawowy parametr związany z pochłanianiem energii, jakim jest SAR. To skrót od Specific Absorption Rate, czyli swoiste tempo pochłaniania energii – to wielkość mówiąca nam ile energii pochłanianej jest przez daną masę w czasie, stąd jednostka W/kg (bo energia na czas daje moc). SAR jest proporcjonalne do przewodności elektrycznej, ale odwrotnie proporcjonalne do gęstości, za to proporcjonalne w kwadracie do natężenia pola elektrycznego. Tylko po co nam SAR?
Co to ma do temperatury?
Nasze tkanki różnią się gęstością i zawartością wody, a to znaczy, że różnie będą pochłaniać to samo promieniowanie elektromagnetyczne. Różniąc się składem, różnią się też ciepłem właściwym i przewodnością cieplną, czyli ta sama ilość pochłoniętej energii nie podgrzeje ich do tej samej temperatury. I w końcu – przecież mówimy o żywym organizmie, więc transport ciepła nie będzie się odbywał jak na lekcji fizyki w klasie siódmej, gdzie ciało A (nieruchome, sztywne, jednorodne, niezmienne…) dotyka ciała B i następuje przepływ ciepła wyłącznie na skutek różnicy temperatur… Przez narządy przepływa krew, która pełni rolę termoregulacyjną – jej przepływ może się autonomicznie zwiększać i zmniejszać, aby konkretny narząd ogrzać lub ochłodzić. Tu pojawia się parametr zwany perfuzją, opisujący ilościowo przepływ krwi przez tkankę – duża perfuzja oznacza duży przepływ. Perfuzja ma kluczowe znaczenie w przepływie ciepła w tkance, ale też musimy pamiętać, że sama tkanka jest żywa, zatem przebiega w niej metabolizm generujący ciepło. Jak to wszystko połączyć w całość?
Równanie Pennesa, zaprezentowane w 1948, pozwala obliczyć wzrost temperatury przy znajomości SAR – uwzględniając, że tkanki różnią się parametrami cieplnymi, jak ciepło właściwe, pojemność cieplna i przewodność cieplna:
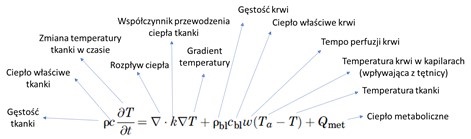
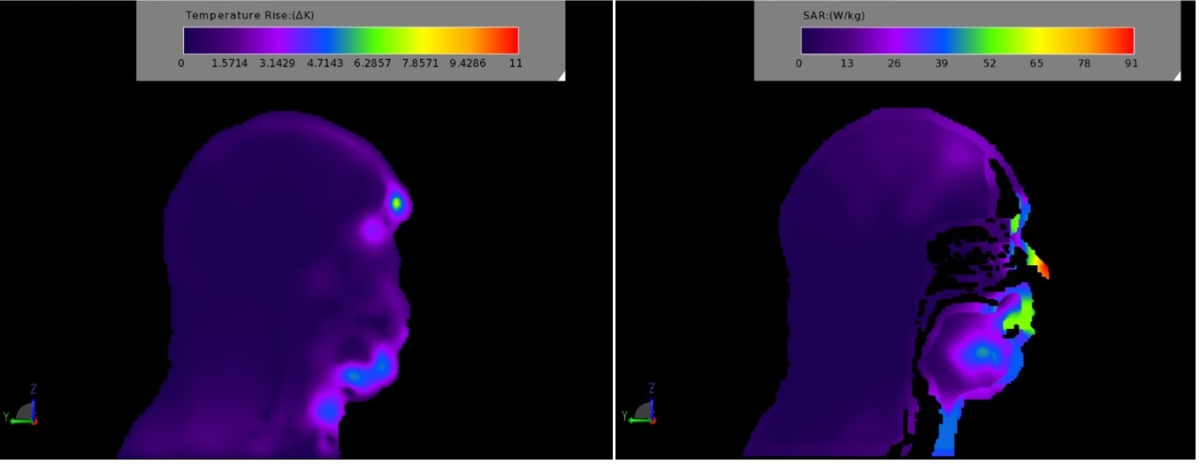
Zostało tylko dodać po prawej stronie równania SAR i gotowe! Mamy generację ciepła w tkance, wymianę ciepła z otoczeniem oraz poprzez krew i dostajemy wynik – i tu ujawnia się istotna sprawa. Widzicie, że SAR i temperatura wcale nie są w zależności y=x? Lokalny wzrost temperatury zależy głównie od typu tkanki, jej ukrwienia i termoregulacji – zatem może się okazać, ze jakieś miejsce, pomimo że otrzymało dużo więcej SAR, wcale się bardziej nie nagrzało…
Jeśli chcecie celnie zwrócić uwagę, że przecież w trakcie ekspozycji nie jesteśmy nieruchomi, albo że w trakcie ruchu nasze tkanki ulegają deformacjom (a więc zmieniają się gęstości oraz zmieniają się przepływy), albo (…i tu wstaw co jeszcze przyszło Ci do głowy…) to tak, inżynierowi i naukowcy o tym też już pomyśleli, czasem kilka dekad temu. Dostępne są nie tylko modele fantomów w różnych pozycjach, ale też fantomy dynamiczne, uwzględniające wspomniane ruchy i deformacje ciała. Mówiąc krótko: naukowcy naprawdę potrafią liczyć i mierzyć!
